Swedish physicist Johannes Rydberg’s discoveries in the field of spectroscopy were largely overlooked during the 19th century. However, in recent times, Rydberg’s work in this area is being explored for its potential use in supercomputers. His research on the hydrogen spectral series laid the foundation for ongoing research by scientists. In celebration of his birthday, let’s explore his early life, work in spectroscopy, and legacy.
A Long Journey Through Academia
Johannes Rydberg was born on November 8, 1854, in Halmstad, Sweden, the only child of Sven Rydberg and Maria Anderson Rydberg. His father was a merchant who died when Rydberg was just four years old, leaving his family struggling financially. He was a good student and developed an interest in mathematics and physics in secondary school. He attended the University of Lund in Sweden, where he received his bachelor’s degree in 1875 and his PhD in mathematics in 1879.
After receiving his doctorate, he remained at the University of Lund for his entire career. His first role at the university was as an amanuensis, or scribe, after which he advanced to the role of docent, or assistant professor, in math and physics. To make ends meet with his modest income as an assistant professor, he also worked as an accountant at a local bank. In 1886, he married Lydia Eleonora Mathilda Carlsson, with whom he had two daughters and a son. He held a range of assistant and temporary professor positions before becoming a full professor of physics at the University of Lund in 1901.

A portrait of Johannes Rydberg taken by Per Bagge. Licensed in the public domain via Wikimedia Commons. Original photograph in the collections of The Archive and Museum of the Academic Society in Lund, Sweden.
Devising the Rydberg Formula
In his research on spectroscopy, Rydberg was trying to determine the wavelengths of photons (of visible light and other electromagnetic radiation) that is emitted by changes in the energy level of an electron in a hydrogen atom. He used wavenumbers to measure the number of wavelengths per unit distance, and in 1888, he was able to arrive at an expression that related the various lines in the spectra of chemical elements. He called this expression the Rydberg formula:
\pm \frac{n}{N_0} = \frac {1}{(m_1+\mu_1)^2} – \frac {1}{(m_2+\mu_2)^2}
In this expression, n is the observed wavenumber, N_0 is a constant for all spectral series and elements, and the rest of the values represent integers indexing the various lines. Over time, physicists have further developed his original equation, and it is now more often used in this form:
\frac{1}{\lambda_{vac}} = R_{\text{H}}\left(\frac{1}{n\tiny{\overset{2}{1}}} – \frac {1}{n\tiny{\overset{2}{2}}} \right)
The hydrogen spectral series defines how the spectrum of frequencies emitted by electrons transitioning from a high-energy state to a low-energy state have been divided into a number of spectral series. These spectral series are important for detecting the presence of hydrogen and calculating shifts of increased wavelengths and decreased frequency and energy. Rydberg’s work connected different series in the spectrum of the same element — namely, hydrogen — into one system that could be represented by a formula.
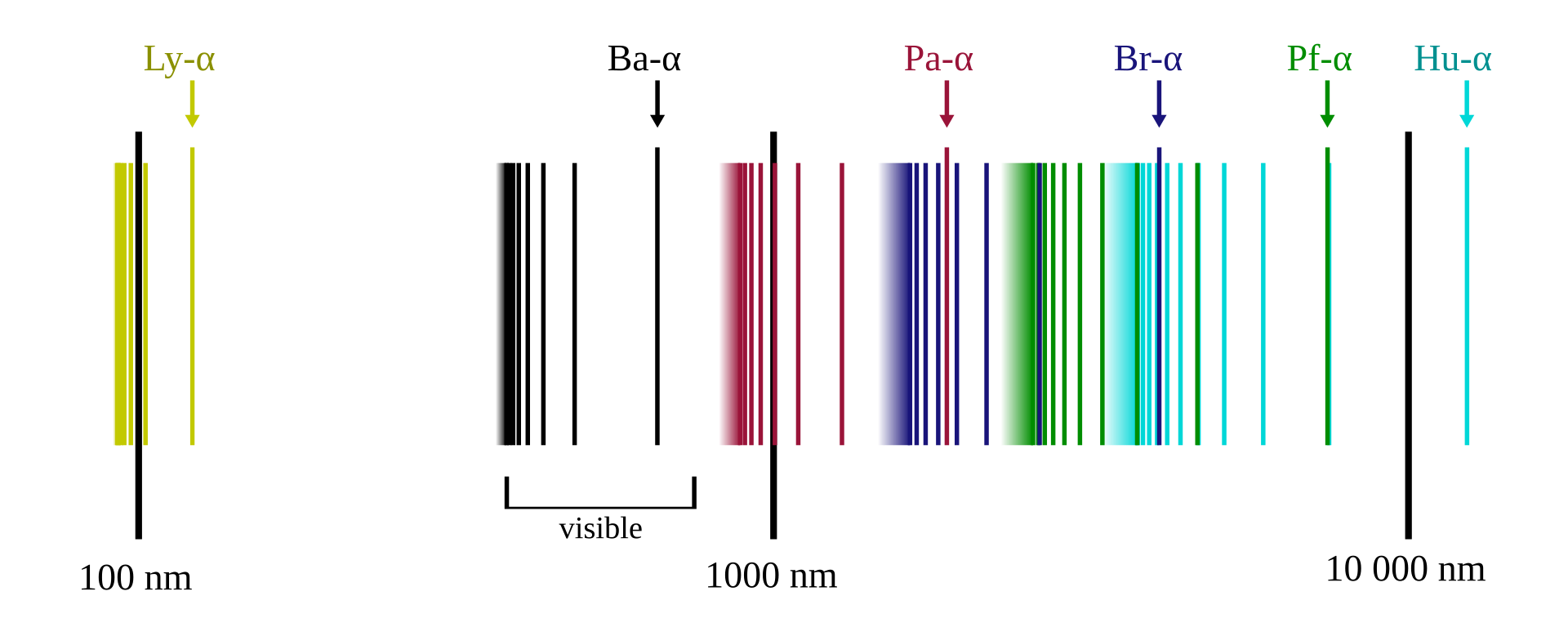
The spectral series of hydrogen, on a logarithmic scale. Illustration by OrangeDog, CC BY-SA 3.0. Licensed under Creative Commons via Wikimedia Commons.
The expression includes a constant term that became known as the Rydberg constant. This constant is a physical constant relating to the electromagnetic spectra of an atom. Rydberg also devised the Rydberg unit of energy, which corresponds to the energy of the photon whose wavenumber is the Rydberg constant. The Rydberg states of an atom are a series of states with energy levels that follow the Rydberg formula as they converge on an ionic state. The Rydberg formula can also be used to describe the many systems that have an electronic structure similar to that of atomic hydrogen. After devising the formula in 1888, Rydberg’s principal published work appeared in a paper titled Research on the Constitution of the Spectral Emissions of the Chemical Elements in 1890.
Rydberg’s Legacy
Rydberg’s theory began to receive acceptance in the early 20th century, when other prominent physicists such as Niels Bohr and Theodore Lyman corroborated it with their own research. He held the University of Lund’s chair of physics position until poor health forced him to take a leave of absence in 1914. He officially resigned the following year and remained in ill health until his death on December 28, 1919, at the age of 65. His former student Manne Siegbahn succeeded his position after his death and later wrote a biography on him.
He was nominated for the Nobel Prize for physics in 1917 and 1920 but did not win either year. In 1919, he was elected to the Royal Society of London. He was also awarded several honors posthumously, including having an asteroid and crater on the moon named after him.
The classification of spectral lines in hydrogen atoms created by the Rydberg formula played a key role in the development of quantum mechanics. This is because it provides strong scientific evidence of quantized energy levels within atoms, which is a fundamental principle of quantum theory. Rydberg atoms have also been instrumental in the research and development of supercomputers, due to their immense ability to perform calculations beyond the limits of the traditional computer. The Rydberg states of an atom allow for strong interactions with nearby atoms, and those strong interactions enable the creation of quantum entanglement, which is a key component of quantum computing.
Further Reading
- Learn more about how Rydberg made a name for himself in the physics world here:
- Read about other featured scientists on the COMSOL Blog:
- Niels Bohr, a Nobel-prize-winning physicist who helped form the basis for early quantum theory
- Max Planck, a contemporary of Rydberg who is best known as the originator of quantum theory
- Henry Cavendish, a physicist and chemist credited with the discovery of hydrogen